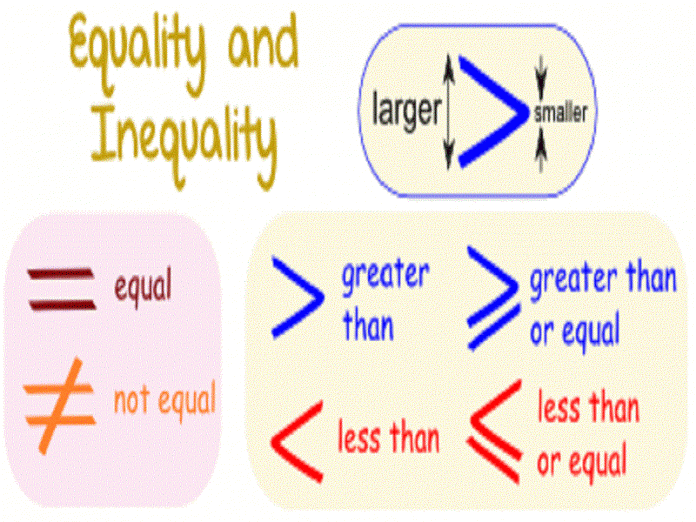Dear Friends,
We team Sehpaathi got to know that many of our visitors find too much trouble while solving the Reasoning Section whenever appeared for any banking exams.So, we took an initiative to come up with our new concept i.e. IBPS Special in which we will provide you all necessary shortcuts,concepts, tricks with problems for each topic of Reasoning. So, we are here with the stuff related to “INEQUALITY”.
Inequality is a common topic for all competitive exams. We can expect 5 or 6 questions from this topic in Reasoning section. It is one of the easy topics for people who are slightly comfortable with elementary mathematics.
So let us try to understand the basics related to this topic.In inequality questions one statement is followed by some conclusions.
In the statement, relationship between some of the variable is given while in the conclusion, relationship between the variables for which the relationship was not given in the statement is given.
We have to analyse the statement carefully to conclude whether the relationship given between the variables in conclusion is correct or not.
Meaning of different symbols
Before getting deep into the inequality, let us try to understand the meaning of the basic operations used in equality –
(1) ‘>’ symbol: This symbol indicates that variable on the left side is definitely greater than the variable on the right side of the symbol.
For example: A>B means A is definitely greater than B.
(2) ‘<’ symbol: This symbol indicates that variable on the left is definitely smaller than the variable on the right side of the symbol.
For example: A<B means A is definitely smaller than B.
(3) ‘=’ symbol: This symbol indicates that variable on the left side is equal to the variable on the right side of the symbol.
For example: A=B means A is definitely equal to B.
(4) ‘≥’ symbol: This symbol indicates that variable on the left side is either greater than or equal to the variable on the right side of the symbol.
For example: A≥B means A is either greater than B or equal to B.
(5) ‘≤’ symbol: This symbol indicates that variable on the left side is either smaller than or equal to the variable on the right side of the symbol.
For example: A≤B means A is either smaller than B or equal to B.
Golden Rules of Inequalities
The combination between two inequalities can be established, if they have a common term.
For e.g.
(i) A > B, B > C – combination can be easily established as: A > B > C. Here we can make conclusion – A > C or C < A
(ii) A < B, B < Q – combination can be easily established as: A < B < Q. Here we can make conclusion – A < Q or Q > A
(iii) A > B, B > C combination can be easily established as: A > B > C. Here we can make conclusion – A > C or C < A
The combination between two inequalities cannot be established, if they don’t have a common term.
For e.g.
(i) A > B, B < C – combination cannot be established. (Here relationship between A & C cannot be established.)
(ii.) A <B, B > D – combination cannot be established. (Here relationship between A & C cannot be established.)
(iii.) A > B, B < C combination cannot be established. (Here relationship between A & C cannot be established.)
The combination between two inequalities can be established, if and only if the common term is greater than (or ‘greater than or equal to’) one and less than (or ‘less than or equal to’) the other.
For e.g.
(i) A > B, C < B. (Here common term B is less than or equal to one term A, and greater than other term C.So here combination between the elements can be easily established.)
A > B, C < B
Possible inequality – A > B > C or C < B < A
Note: Here we can make conclusion as: A > C or C < A
(ii) P > Q, Q < C – (Here common term Q is less than both the term, so combination between the elements cannot be established.)
(iii) N > M, L > N (Here common term N is greater than or equal to one term M, and less than other term L. So here combination between the elements can be easily established.)
N > M, L > N
Possible inequality – L > N > M or M < N < L
Note: Here we can make conclusion as: L > M or M < L
(iv) N > M, N > L (Here common term N is greater than both the term, so combination between the elements cannot be established.)
If we combined the inequality – L < N > M; so here we cannot make combined inequality.)
Complementary Pairs: (Either & or) – Either and or cases only takes place in complementary pairs. We cannot combine two elements with common elements in which no relation is established.
For e.g.
A > B, B < C
1. Statement: A > B < C
Conclusion: I. A > C II. A < C
Here we cannot establish relation between A and C. We can only draw conclusion i.e. A is either greater than or equal to C or we can say A is either smaller than C.
From the given above conclusions, it is easy to understand that one of the given conclusions must be true, which is represented by option either (i) or (ii). These types of pairs are called complementary pairs.
One more complementary pair is < and >. These two relations covers the entire possibility same as > and <.
2. Statements: A = B > C > D < E
Conclusions: I. A > C II. A = C
Conclusion doesn’t form the complementary pairs but still here the answer is either-or because only two relations can be established between A and C. Here conclusion either I or II follows, because here we can say A is either greater than C or equal to C.
3. Statements: A = B > C > D < E
Conclusions: I. A > E II. A < E
Here, conclusion either I or II follows. We don’t know the exact relation between A and E. Here A can be either greater than E or Smaller or equal to E.
Key points related to Inequality:
- First step is to decode the statements (if the problem is on coded inequality)
- Second step is to write the least possible group of outcomes.
- Last step is to check whether the given conclusions follow or not on the basis of outcomes.
- All >, =, ≥ come in a single group of outcome.
- All <, =, ≤ come in another group of outcome.
- If any variable is not in both of the groups then we can’t define the relation between those variables.
PRACTICE EXERCISE
Do share us your reviews with us regarding our new initiative….. 🙂